My econometrics class has about 150 students, and that’s exactly the capacity of our regular classroom. It works fine for lectures since not everyone shows up and I want them sitting close together as they work through problems. For our midterm exam, however, this would have been just awful. Luckily, I was able to additionally reserve the room across the hall that holds 170. This let me split the class evenly between the two rooms and give everyone space to breathe. And because I used random assignment, I had a natural experiment to test the effect of location on exam performance.

There’s some research in psychology that says that people remember things better when they are in the location where they learned them, though my cursory Google search didn’t turn up any references. If true, I would expect the test scores of those students who took the exam in our original classroom (LC-101) to be higher than those of students across the way in LC-102. On the other hand, we had some issues with the room lighting on exam day in LC-101: It was a little dark until about halfway through the exam when some facilities folks came by and showed us how to turn up the lights. My expectation (and hope) was that these two minor effects would offset each other.

Here’s what actually happened:

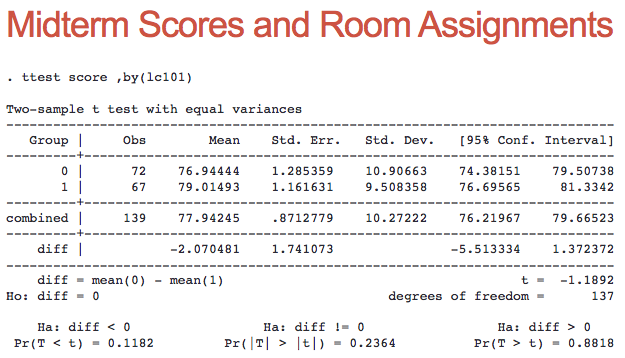
Test scores of students taking the exam in our regular classroom were on average about two points higher (79 vs. 77) than those of students across the hall. The p-value of the test was 0.24. That means that if the true classroom effect was zero and I held the exam 100 times, I would expect a difference in average scores of at least two points (what I observed) about 24% of the time due to random variation in student performance. So while there might be a real classroom effect, this experiment doesn’t provide much evidence for it. In most academic research, we wouldn’t consider the effect statistically significant unless that p-value was below 0.05.

Beyond the substantive cognitive psychology question, there’s an interesting ethical question here: What if that p-value had been below 0.05? Should the scores of the students in the alternative classroom be adjusted upward to compensate for their disadvantage? I’m really glad I don’t have to answer it now, but I’d love to have an answer for the future.