On Wednesday I had lunch with five students from my 130 person econometrics class. These were the five that responded to the invitation I had sent to everyone the day before. Over lunch I asked what they thought of the date for the upcoming midterm exam. They universally hated it.

The midterm was scheduled for Monday, October 19. Yale’s October Break gives everyone the rest of the week off. Having the exam that week means my students can’t skip class and take off the whole week. Two of my lunch students had other exams the same day and were not looking forward to pouring both classes into their head during the weekend before. All five students said they wouldn’t mind studying over break if they could take the midterm on the Monday after. I know five is a small sample, but it sure seemed like moving the exam would make a lot of students happy and wouldn’t be a big deal for me.

On the other hand, it’s best to be sure, so I polled the class with a clicker question at the beginning of my next lecture:

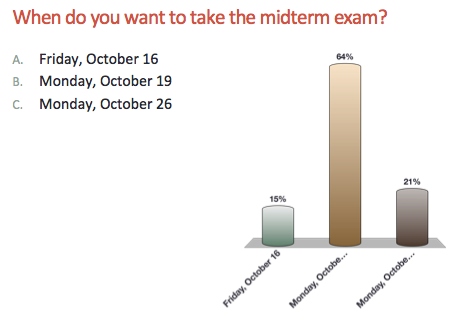
64% of the class wanted to leave the exam right where it was. What the heck happened? In hindsight, this is a classic case of selection bias. Using the methods I teach in this class, it’s not hard to show that the probability of five randomly selected students saying they want to move the exam when 64% like the current date is an incredibly unlikely 0.006 (i.e., 0.36^5).

The problem was that my lunch group was far from a random sample. These are five of the most engaged students in the class. Of course they wanted more time to study for the exam even if it meant giving up some peace of mind over their break.

The lesson here is kind of obvious: Small non-random samples often don’t reflect what’s going on in with a class as a whole. Before you make a big change (like moving an exam) you should verify your “facts” with a survey or at least a show of hands during lecture.